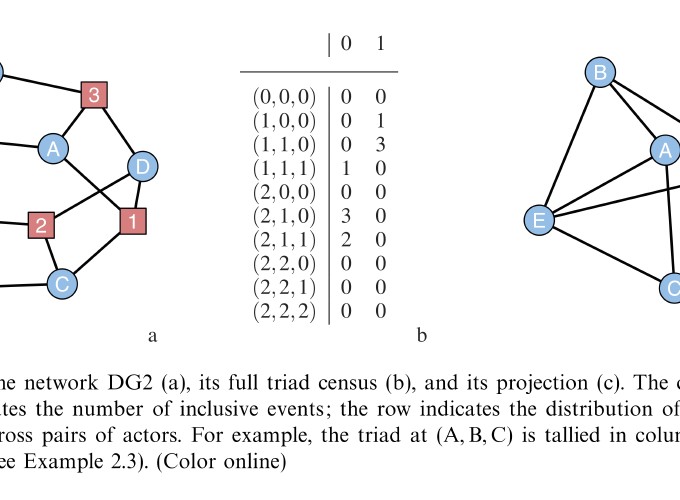
Abstract

Triadic closure has been conceptualized and measured in a variety of ways, most famously the clustering coefficient. Existing extensions to affiliation networks, however, are sensitive to repeat group attendance, which does not reflect common interpersonal interpretations of triadic closure. This paper proposes a measure of triadic closure in affiliation networks designed to control for this factor, which manifests in bipartite models as biclique proliferation. To avoid arbitrariness, the paper introduces a triadic framework for affiliation networks, within which a range of measures can be defined; it then presents a set of basic axioms that suffice to narrow this range to the one measure. An instrumental assessment compares the proposed and two existing measures for reliability, validity, redundancy, and practicality. All three measures then take part in an investigation of three empirical social networks, which illustrates their differences.